How to Calculate Compressible Gas Flow in Pipes

Compressible Flow in Pipes – Adiabatic, Isothermal, and Polytropic Relations

In compressible flow, exact relation between pressure and specific volume is required, but it is not easily determined in each specific problem. Usually extremes are considered like adiabatic and isothermal flow.

Adiabatic compressible flow is the flow where no heat is transferred to or from pipe like in short, perfectly insulated pipe. The heat which is created due to flow friction is added to the flow and that amount of energy is actually acceptable. For adiabatic compressible flow is:

where is:

p - pressure; V - volume; γ - isentropic coefficient;

Isothermal compressible flow is the flow at constant temperature. Isothermal compressible flow often more closer to fact in piping transportation systems like in natural gas lines.

where is:

p - pressure; V - volume;

Other relation between pressure and specific volume are called polytrophic and interpretation for each individual case is almost impossible.

where is:

p - pressure; V - volume; n - polytrophic exponent;

The density of gases changes with the change in pressure considerably, so if the pressure drop in pipe is great the density change will also be great and Darcy formula should be applied with following restrictions:

• If the calculated pressure drop is less than about 10% of the inlet pressure, Darcy formula can be used with reasonable accuracy and specific volume should be used either on the upstream or on the downstream conditions,
• If the calculated pressure drop is greater than about 10% and less than about 40% of inlet pressure, the Darcy equation may be used with reasonable accuracy by using a specific volume based upon the average of upstream and downstream conditions,;
• For pressure drops higher than 40% of inlet pressure, as in long pipe lines, other formulas should be used.

Isothermal Compressible Gas Flow – Pressure Drop, Flow Rate, and Friction Factor

The flow in long pipelines closely approximates isothermal conditions. The pressure drop in such lines is often large compared to inlet pressure and solution of this problem is outside the limitations of the Darcy equation. An accurate solution is made by compressible isothermal equation where weight flow w in [kg/s] is:

where is:

p_1,2 - pressure on the begging and on the end of pipe line; w - mass flow rate; v₁ - specific volume; f - friction factor; L - pipe length; D - internal pipe diameter; A - pipe cross section area;

Substituting specific volume using equation of state pressure drop due to friction can be written as:

where is:

p_1,2 - pressure on the begging and on the end of pipe line; w - mass flow rate; Z_m - mean compressibility factor; R - gas constant; T - temperature; f - friction factor; L - pipe length; D - internal pipe diameter; A - pipe cross section area;

Both two above equations are developed with following assumptions:

• flow is isothermal,
• no mechanical work is added or subtracted,
• flow is steady in time,
• gas is perfect,
• velocity is represented as the average velocity in cross section,
• the friction factor is constant,
• pipe line is straight and horizontal,

In the practice of compressible gas pipe line engineering, another assumption is added:

Acceleration can be neglected because the pipe line is long.

With that assumption, equation for compressible isothermal flow in horizontal pipe line is:

or:

where is:

p_1,2 - pressure on the begging and on the end of pipe line; w - mass flow rate; v₁ - specific volume; f - friction factor; L - pipe length; D - internal pipe diameter; A - pipe cross section area; Z_m - mean compressibility factor; R - gas constant; T - temperature;

Mean compressibility factor is calculated as:

where is:

Z_m - mean compressibility factor; Z₁ - compressibility on the begging of pipeline; Z₂ - compressibility on the end of pipeline;

Volumetric flow rate can be calculated for defined conditions, like normal conditions, standard conditions or based on the actual flow condition used appropriate density in following equation:

where is:

q - volumetric flow rate; w - mass flow rate; ρ - density;

• Normal conditions: p=101325 Pa, T=273,15 K;
• Standard conditions: p=101325 Pa, T=288,15 K (15^OC)

When volumetric flow at specified condition is known, using continuity equation volumetric flow rate on some other condition can be calculated using:

where is:

q - volumetric flow rate; p - pressure; T - temperature;

As it is usually more common to express flow rates in terms of cubic meter per hour at standard conditions equation for isothermal compressible flow can be written:

where is:

q_h - volumetric flow rate [m₃/h]; p - pressure [Pa]; T - temperature [K]; S_g - relative density [ - ]; L_m - pipe length [km]; d - internal pipe diameter [mm]; f - friction factor [ - ];

Weymouth and Panhandle Equations – Empirical Formulas for Natural Gas Flow

Other equations are used for compressible flow in long pipe lines like Weymouth and Panhandle formula:

Weymouth formula is:

where is:

q_h - volumetric flow rate [m₃/h]; p - pressure [Pa]; T - temperature [K]; S_g - relative density [ - ]; L_m - pipe length [km]; d - internal pipe diameter [mm];

Friction factor used in Weymouth formula is: f=0.094/d ^1/3. This friction factor is identical with one obtained from Moody diagram for fully turbulent flow for 20 inch inside diameter. For pipe diameters that are smaller than 20 inch, Weymouth friction factors are larger and for pipes bigger than 20 inch, Weymouth friction factor is smaller than in friction factors obtained from Moody diagram for same pipe sizes.

Panhandle formula is:

where is:

q_h - volumetric flow rate [m₃/h]; p - pressure [Pa]; L_m - pipe length [km]; d - internal pipe diameter [mm]; E - flow efficiency factor E=0.92;

Panhandle formula is for natural gas pipe sizes from 6" to 24", and for Reynolds numbers between Re = 5x10⁶ and Re = 14x10⁶, with specific gravity for natural gas S_g=0,6. The flow efficiency factor E is defined as an experience factor and is usually assumed to be 0.92 for average operating conditions.

The Panhandle friction factor is defined as: f = 0.0454 (d/q_hS_g)0.1461. In the range where Panhandle formula is applicable, the friction factors are smaller than one from Moody diagram as because of that the flow rate are usually greater than those calculated using equation for isothermal flow.

Renouard Equation – Pressure Drop and Flow Rate for Natural Gas Pipelines

Calculation of compressible natural gas flow and pressure drop through natural gas pipe line can be made using Renouard equation:

where is:

p₁ - absolute pressure on the start of pipe line [bar]; p₂ - absolute pressure on the end of pipe line [bar]; S_g - relative density [ - ]; L - pipe length [km]; q_h - volumetric flow rate [m3/h]; D - internal pipe diameter [mm] ;

Volumetric flow rate q_h in Renouard equation is to be used at standard conditions (p=101325 Pa, T=288,15 K (15^OC)).

Relative density in Renouard equation is calculated as follows:

where is:

S_g - relative density (around 0.64 kg/m³); ρ_NG - natural gas density on standard conditions, which depends on the natural gas mixture (around 0.78 kg/m³); ρ_AIR - air density at standard conditions, which is 1.226 kg/m³;

Maximum Flow Rate and Gas Velocity – Sonic Flow and Expansion Factor (Y)

When the pressure on the downstream of the gas flow reaches certain value, further pressure decrease at the end will not cause higher weight rate of flow [kg/s]. It means that the gas flow in the pipe has its maximum depending on the available energy on beginning. If the pressure drop is sufficiently high, the exit gas velocity will reach the speed of sound, and maximum weight gas flow rate will occur. Further pressure drop and pressure decrease on the outlet will not be felt upstream because the pressure wave can only travel as sonic velocity and the "information" about pressure drop will never translate upstream. Shock waves will occur but actual gas weight flow rate will not increase. The maximum possible gas velocity in the pipe is sonic velocity, which is expressed as:

where is: v_s - velocity of sound; γ - isentropic coefficient; R - gas constant; T - temperature;

In the case of the gas compressible flow through a short pipe into the area with larger cross section, or into the atmosphere, the flow is usually considered to be adiabatic. For this situation Darcy formula should be used with factors to compensate on the fluid changes due to expansion, using expansion factor Y. Modified Darcy formula with expansion factor included is then:

where is: w - mass flow rate [kg/s]; Y - expansion factor [ - ]; d - internal pipe diameter [mm]; Δ p - pressure difference [Pa]; ρ - density [kg/m³]; K - total resistance coefficient [ - ];

The value K in this equation is the total resistance coefficient of the pipe line, including entrance and exit losses when they exist, and losses due to valves and fittings. In above equation the pressure difference Δ p is the difference between inlet pressure and the pressure on the larger cross section. When compressible fluid is flowing into the atmosphere it is equal to gauge inlet pressure.

When the pressure difference Δ p between inlet pressure and the larger cross section area pressure, or the atmosphere pressure, is higher than the value in the table below, for certain value of resistance factor K, the flow will be sonic on the exit or somewhere along the pipe and expansion factor Y will be as it is given in table bellow.

For other values of pressure drop Δ p, tables bellow should be used for expansion factor Y determination based different values of resistance factor K. Note - all tables for expansion fact determination can be used for perfect gases.

Heat Energy from Fuel Combustion – Power Output and Efficiency

Heat energy in unit of time (heat power) from combustion of fuel can be calculated as:

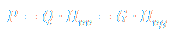
where is:

P - heat energy in unit of time - heat power; Q - volume flow rate; G - mass flow rate; H_vv - heat value in unit of energy per unit of volume H_vg - heat value in unit of energy per unit of mass

Relation between volume and mass flow rate is calculated as:

where is:

ρ - density

Due to fact that part of total energy created by combustion is not converted to useful energy, coefficient of efficiency is introduced - η and its value is between 0 and 1. Actual power P₁ that can be used from fuel combustion is calculated as:

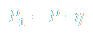
where is:

η - efficiency

Heat values of fuels can is available in terms of energy per unit of volume or as energy per unit of mass. Relation between them is:

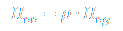
Flow of Dry or Saturated Steam – Heat Energy and Phase Change Fundamentals

Under normal atmospheric conditions exists in the form of liquid. When the heat energy is added to the water the temperature of water rises and at certain temperature, depending in the value of pressure, boiling starts.

If the heat energy is added after the boiling starts, the temperature of water will not rise until whole amount of water evaporates. This state is called saturated steam, as at the same time both state of water are existing - liquid and steam state. It may be wet or dry saturated steam. The dry saturated steam does not contain mechanically mixed liquid water particles, as wet does. So actually with heat being added to the water after the boiling starts, the wet saturated steam will change state into dry saturated steam, due to evaporation of liquid particles in the mixture of steam and liquid.

If the heat energy is being added just after the whole water has evaporated and the steam is in the state of dry saturated steam, the temperature and pressure of steam will start to rise and this state is called superheated steam.

Heat energy is the form of energy and unit for heat in metric system is the joule [J]. As it is very small unit, more often is used kilojoule [kJ] or even larger megajoule [MJ]. Energy per unit mass is the joule per kilogram [J/kg] or multiple of this unit like [kJ/kg] etc.

The relationship between the joule and the British thermal unit [Btu] is defined by:

1 Btu/lb = 2.326 J/g = 2.326 kJ/kg.